单向链表的反转(递归法)

上次讲了通过迭代法 的方式，新建一个NewL倒叙插入原链表结点来实现反转，这次来讲递归法。

首先，什么是递归，去Google搜递归，会得到一个“你是不是要找递归”的提示，点开后还是这个页面。这就是递归。递归简单说就是函数调用自己。递归思想类似与栈，后入先出。这里重点讲讲递归实现单向链表的过程。

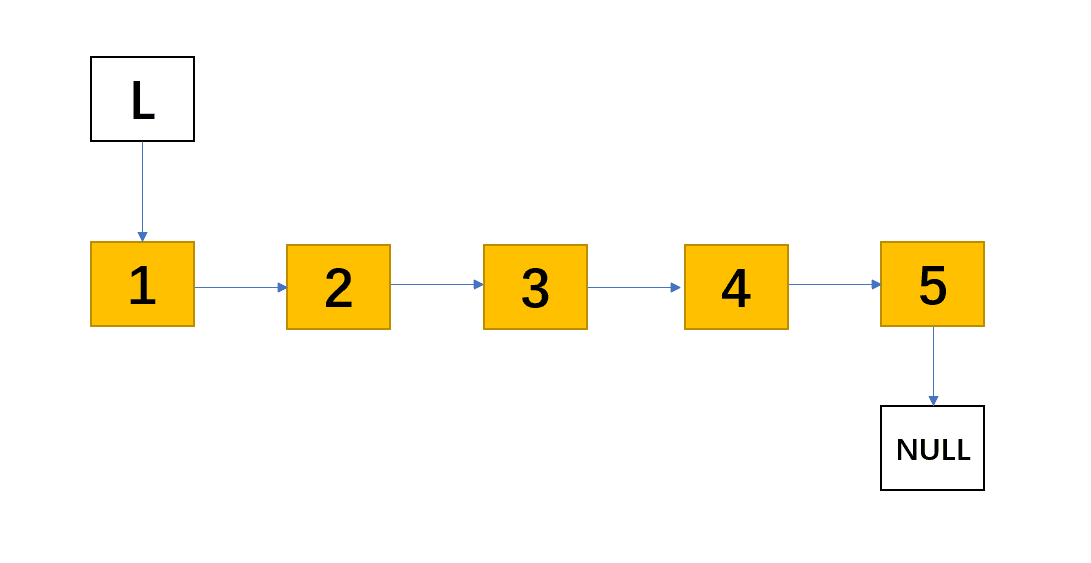
我们还是以这样一个五个元素的单链表为例，注意和之前一样演示的链表包含一个头结点L

//链表的结构
typedef struct Node
{
    int date;
    struct Node * next;
} Node;
typedef Node * LinkList;

递归

递归需要出口，回想斐波拉契数列递归实现，我们的出口是当数字n==1 || n ==2 时，return 1;结束。对于一个单向链表来说，遍历到末尾NULL就是终点，同时考虑空表的情况，所以我们就有了递归的出口：

LinkList In_reverse(LinkList L){
    if(L == NULL || L -> next == NULL)
        return;
    ...
}

递归的问题规模需要逐渐缩小，我们设置递归的前进条件，也就是遍历链表，新建一个新的头结点指针 NewL 让他等于递归结果。

...
    if(L == NULL || L -> next == NULL)
        return;
	LinkList NewL = In_reverse(L -> next);
...

根据递归的出口条件，当 L -> next == NULL时候返回，此时L就在5的位置，姑且称他为L=5的时候(而不是L指向5这个结点,指向5结点的是其前继4）。同时在递归结束前NewL也等于5，也就是说此时L，NewL都在最末尾的结点。同时因为递归调用已经结束，所以在接下来递归回退的过程中 LinkList NewL = In_reverse(L -> next) 不会再执行，NewL始终留在原链表的最后结点。

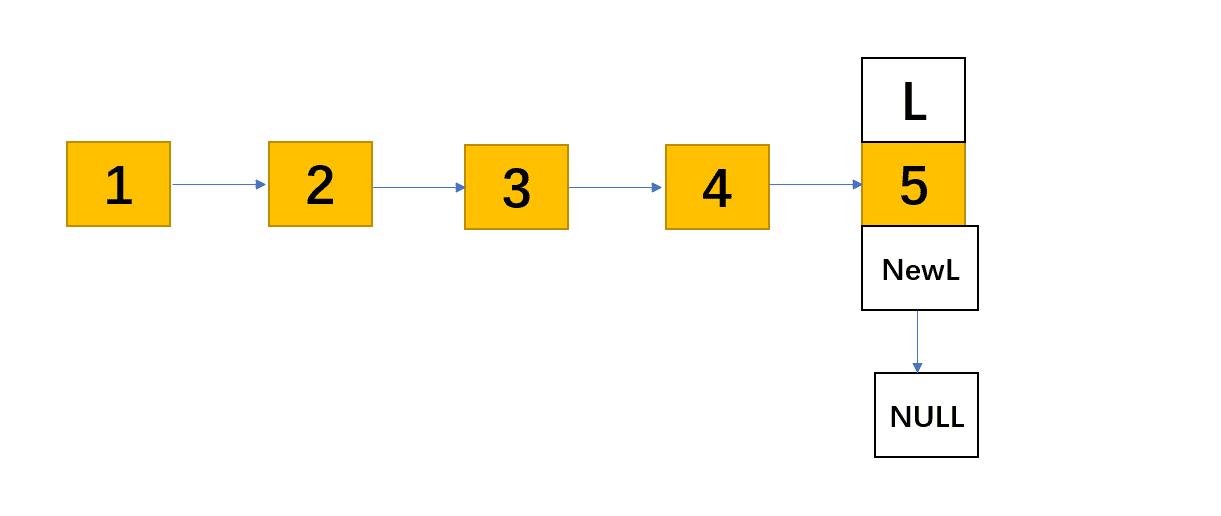
既然递归结束了就要开始退回，根据后进先出的原则，首先回到的是L = 4的时候，开始执行递归调用后的代码

所以我们需要做什么？我们希望的结果是逆序原来的链表，现在的情况是我们创建的NewL已经牢牢地呆在原链表的最末尾也就最后新链表的开始，这正是我们想要的，所以我们只需要让4结点和5结点反一下指向不就实现了逆序。

为了实现反序，让后继的后继等于我，此时4结点和5结点是成环状态，互相指向对方。

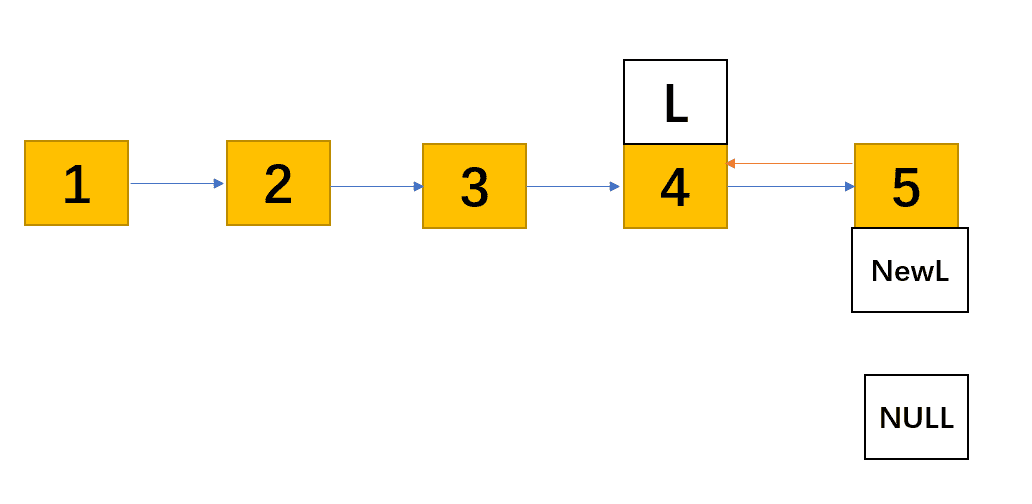
代码实现上我们让5结点的next指向L，5结点也是4结点（同时也是现在的L）的后继，所以可以

L -> next -> next = L;

再让原本4结点的后继指向NULL，也就是反序后新链表的表尾，同时破除了两节点的环。

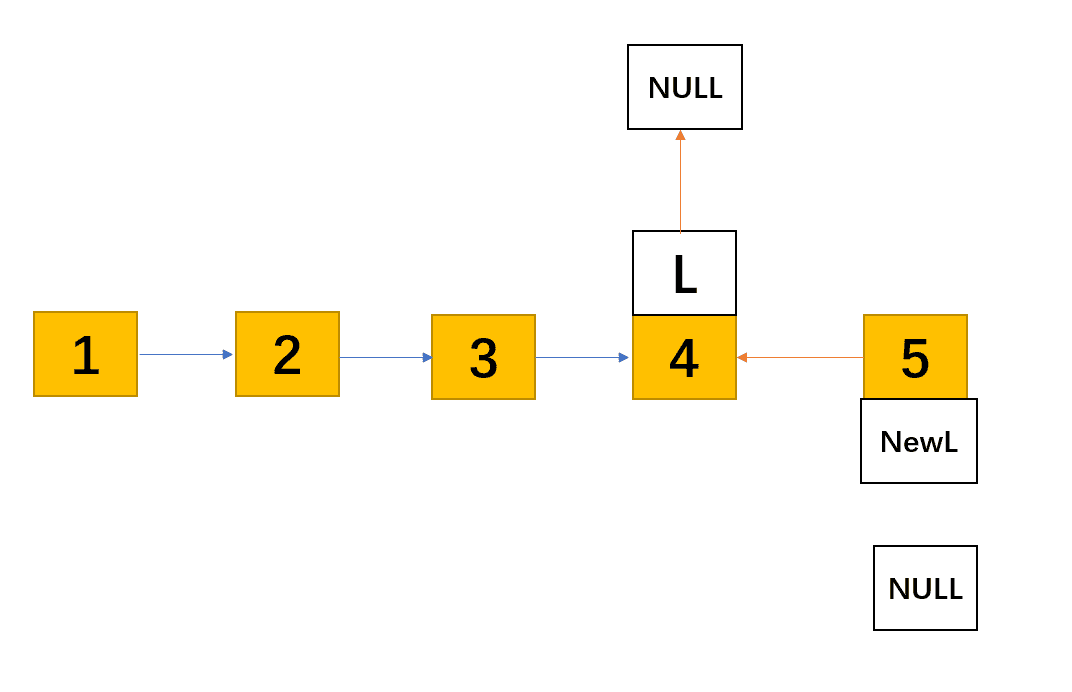
L -> next = NULL;

这样一个5(NewL)->4(L)->NULL 的链表就形成了。

实现

所以递归法的代码就是：

LinkList In_reverse(LinkList L){
    if(L == NULL || L -> next == NULL)
        return;
    LinkList NewL = In_reverse(L -> next);
    L -> next -> next = L;
    L -> next = NULL;
}

代码结束了，递归的回退过程还在进行，继续探讨这个过程，此时函数回退到L遍历到3结点的时候，因为第4行已经执行过了，所以从第五行开始。

和刚才一样我们让3结点的后继指向自己，同时自己指向NULL，现在得到了新的链表5(NewL)->4->3(L)->NULL

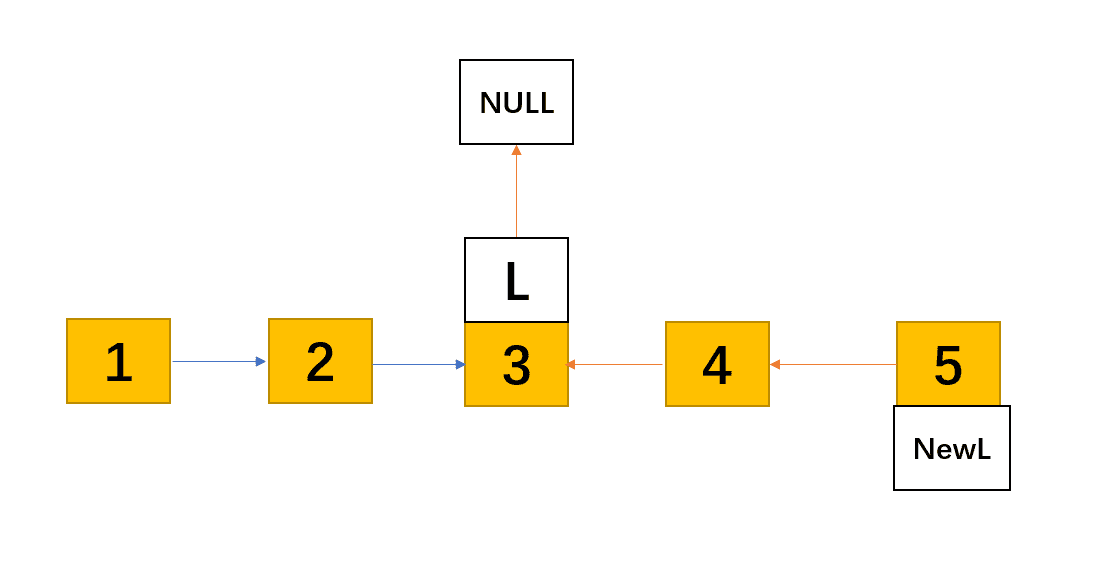
递归继续回退到L=2时候，得到新的链表5(NewL)->4->3->2(L)->NULL

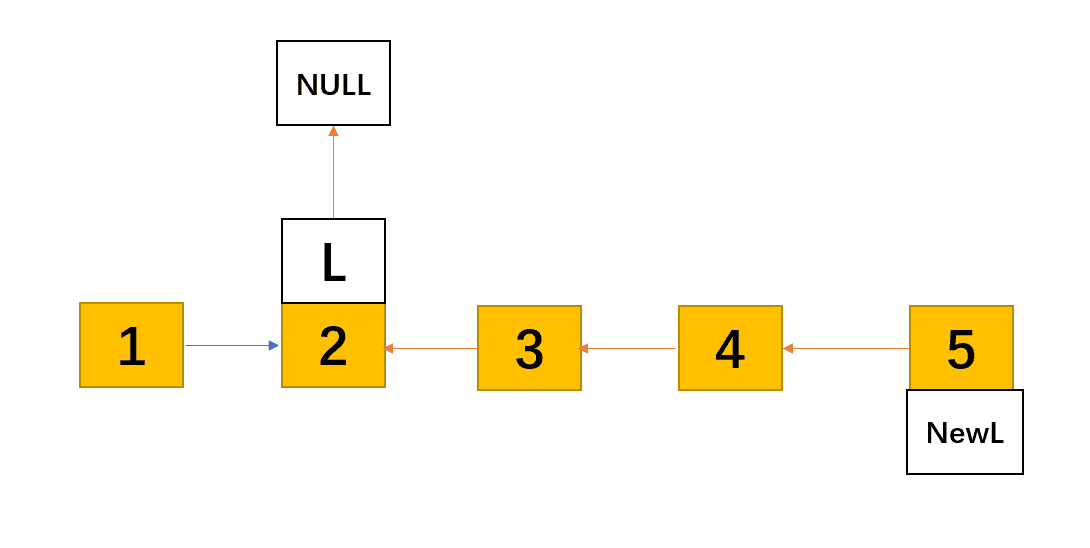
终于函数回退到了它递归开始的时候 ，此时L = 1，（注意：对于带有头结点的单链表在传入时应该是其第一个元素而不是空数据域的头结点），其他操作还是和之前一样，最终我们就得到了原单链表的反序链表5(NewL)->4->3->2->1(L)->NULL

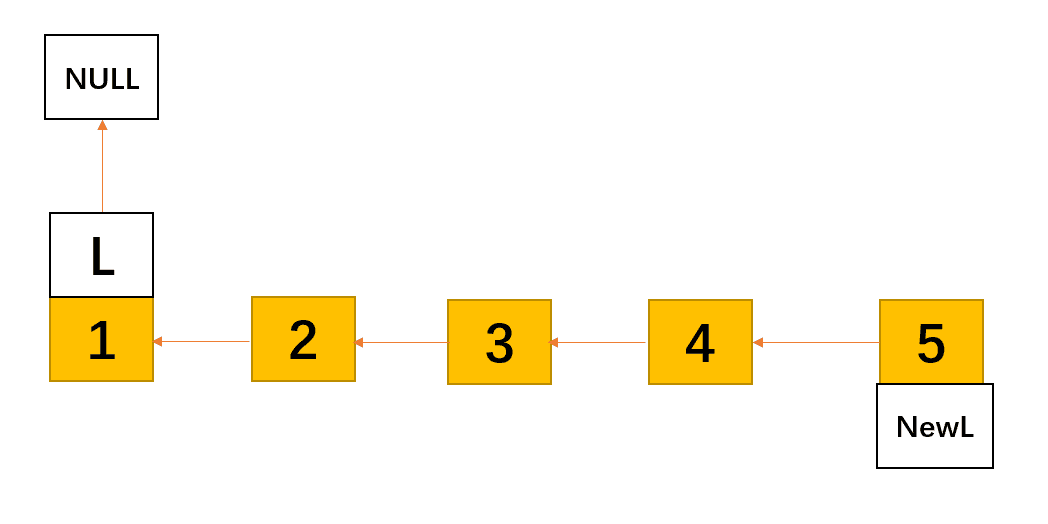
细节

前面我们提到在传入带有头结点的单链表时候一定要是其第一个元素，而不是头结点，因为考虑如果传入的是头结点，那么当L=1执行完成后，在函数递归回退过程中还存在L为头结点的时候，同样也会让一个没有数据域的头结点加到了反序的单向链表中，中间出现无关结点并不是我们希望的。

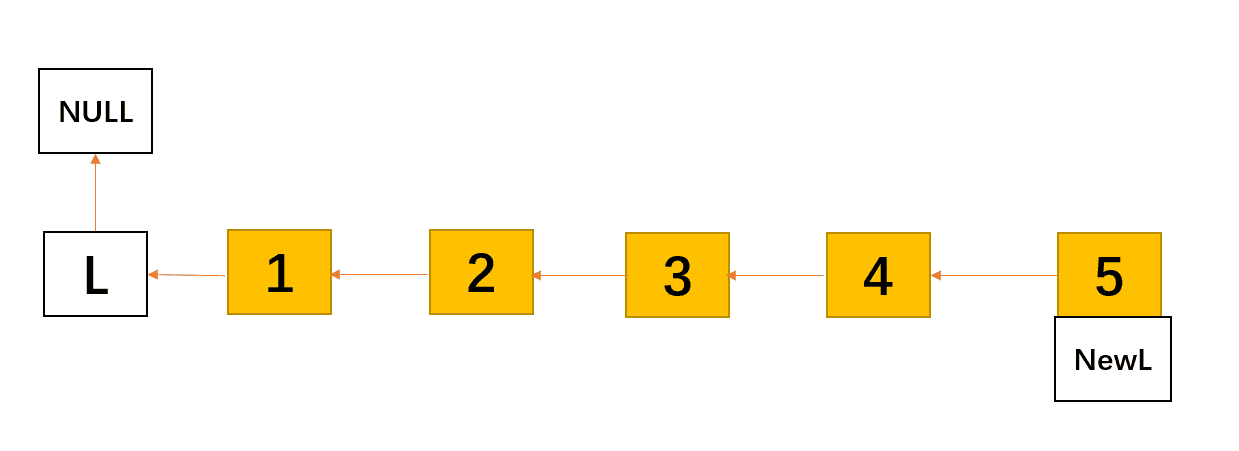
对于存在头结点的单链表在函数的调用时候传入其后继，同时因为反序后的链表没有头节点，所以让原单链表的头结点指向反序后的首元素即可。原来适用于带头结点的遍历函数同样适用。

int main(void){
    ...
    L -> next = In_reverse(L -> next);	//带有头结点的链表需要传入其第一个元素
//	L = In_reverse(L);	没有头结点的链表反转
   	display(L);		//接收带头结点的单链表进行遍历
    ...
}

结尾

至此关于单链表反序的两种方法迭代法和递归法就介绍完了，仔细想想虽然简单但其背后的逻辑确实精美巧妙，每次理解完前人写得经典算法总是会不由得感慨他们实在是聪明，解决抽象问题就像计算机思维一样思考。

If I have seen further, it is by standing on the shoulders of giants.

Isaac Newton

Asahi
2019.10.23